こんにちは、中学受験ブログを運営しているポチ(@pochi2023)です。
今回は「算数の図形」がテーマです。
現在、息子(小5)は日能研で「図形」の単元を学習しています。
学習の様子を見ていて感じるのですが、かなり覚えることが多いですね。
公式はもちろんのこと、計算問題でも覚えておくと速く解けるコツがあります。
テストも基本問題に時間をかけすぎて、応用問題の時間が足りなかった〜
今回は「面積」の問題が得意になる秘訣をご紹介したいと思います。基本的なことが多いので、小学5年生向け中心の情報です！
などでお悩みの方々の参考になれば幸いです！
1.多角形の面積で覚えるべきこと
まず最初は覚えるべき基本の公式からです。
もう頭に入っているという方は読み飛ばしてもらって構いません。
| ＜多角形の種類＞ | ＜公式＞ |
| 三角形 | 底辺×高さ÷2 |
| 平行四辺形 | 底辺×高さ |
| ひし形(正方形) | 対角線×対角線÷2 |
| 台形 | (上底＋下底)×高さ÷2 |
「平行四辺形」だけ「÷２」がありませんので注意が必要です。
逆に「ひし形」は「÷２」を忘れがちですので、こちらもご注意ください。
問題は、こうした公式をうまく隠すように作られています。
例えば、底辺が右辺になっていたり、補助線を引かないと三角形が見えてこなかったり。
でもまずは、公式をしっかり頭に入れるところが出発点になります。
この４つの公式が基本になるので、完璧に覚えてから次に進みましょう！
2.「円」「おうぎ形」で覚えるべきこと
続いては「円」と「おうぎ形」についてです。
ここから覚えることが複雑になっていきますね。
まずは基本の４つの公式から。
| 円周 | 直径×3.14 |
| 円の面積 | 半径×半径×3.14 |
| おうぎ形の面積 | 円の面積×中心角／360 |
| おうぎ形の弧 | 円周×中心角／360 |
この中で、特に勘違いをしやすい公式があります。
それが「おうぎ形」の「面積」と「弧」の違いです。
この２つが整理できていない人が多いようです。
息子も塾で教わって帰ってきた当初は、ここが完全に理解できていませんでした。
この違いが分かってなかったので、最初は苦労しました
ここは重要ですので、しっかりと理解しておきましょう。
3.覚えると計算が速くなる「3.14の段」
「図形」の単元で、重要になってくるのが「3.14の段」のかけ算です。
円周率を使って求めるため、頻繁に「3.14」をかける計算が出てきます。
これを「分配法則」を使って計算するのですが、普通に解いていると時間がかかってしまいます。
算数が得意な友人は、この3.14の段の計算を完璧に覚えているそうです。
では一体どこまで覚えておくといいのか、教えてもらいました。
| 3.14×２= | 6.28 |
| 3.14×３= | 9.42 |
| 3.14×4= | 12.56 |
| 3.14×5= | 15.70 |
| 3.14×6= | 18.84 |
| 3.14×7= | 21.98 |
| 3.14×8= | 25.12 |
| 3.14×9= | 28.26 |
9までのかけ算は完璧にしたほうがいいそうです。
さらによく出る数字を教えてもらいました。
| 3.14×12 | 37.68 |
| 3.14×15 | 47.10 |
| 3.14×16 | 50.24 |
| 3.14×25 | 78.50 |
| 3.14×36 | 113.04 |
ここまで完璧にしておくと、かなり計算がスピードアップします。
中途半端な記憶だと計算ミスに繋がるので、これは完璧に仕上げる必要があります。
少し大変ですが覚えておくと一気に計算が早くなり、また計算ミスも防ぐことができます。
我が家は暗記カードを使って、この週末に完璧にしたいと思います。
計算のコツやミスを防ぐ方法は下記の記事にもまとめています。よかったら参考にしてみてください。
面積の問題に限らず、計算が早ければ応用問題に時間をかけられるよ！
4.ライバルと差がつく「図形」３つ
最後に、覚えておくとライバルと差がつく「図形」を３つご紹介しましょう。
問題集やテストなどでもよく見かける図形問題です。
・葉っぱ形&レンズ形
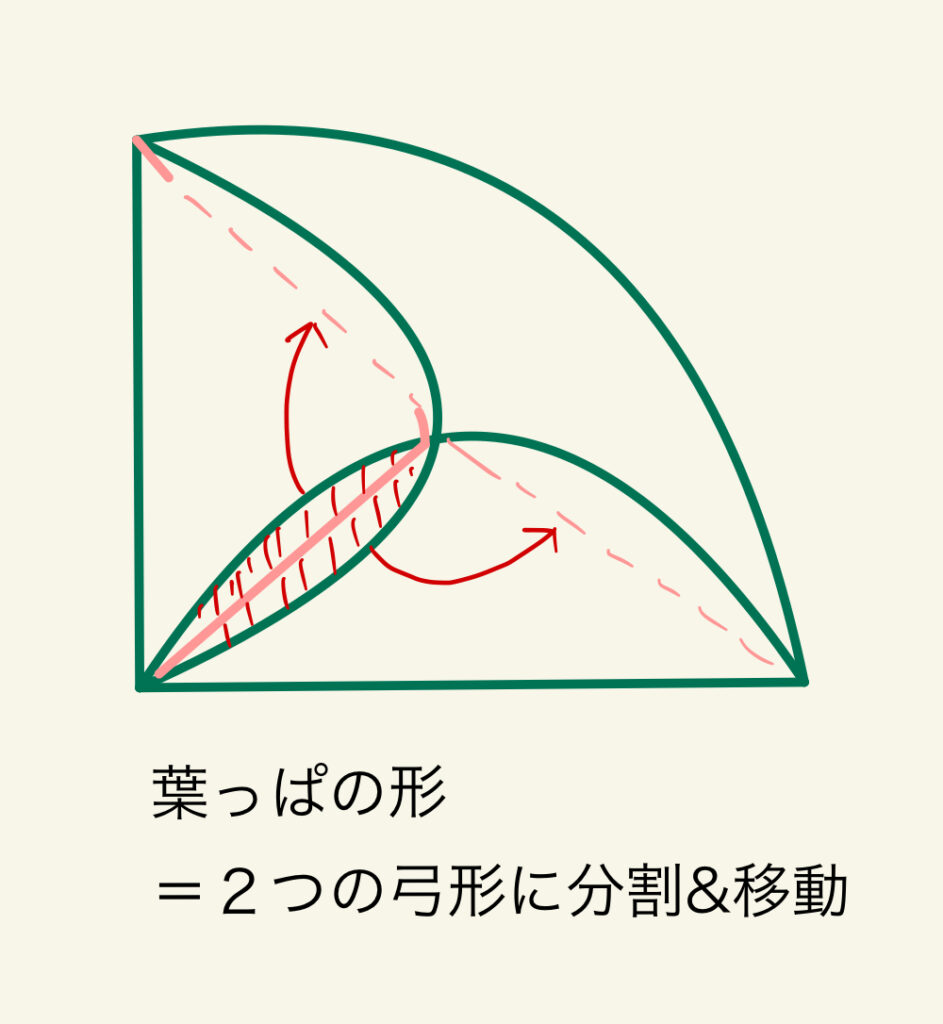
まず最初は「葉っぱ形」(レンズ形)です。
この場合は、図のように分割して移動させると計算がしやすくなります。
・半径がわからない円の面積
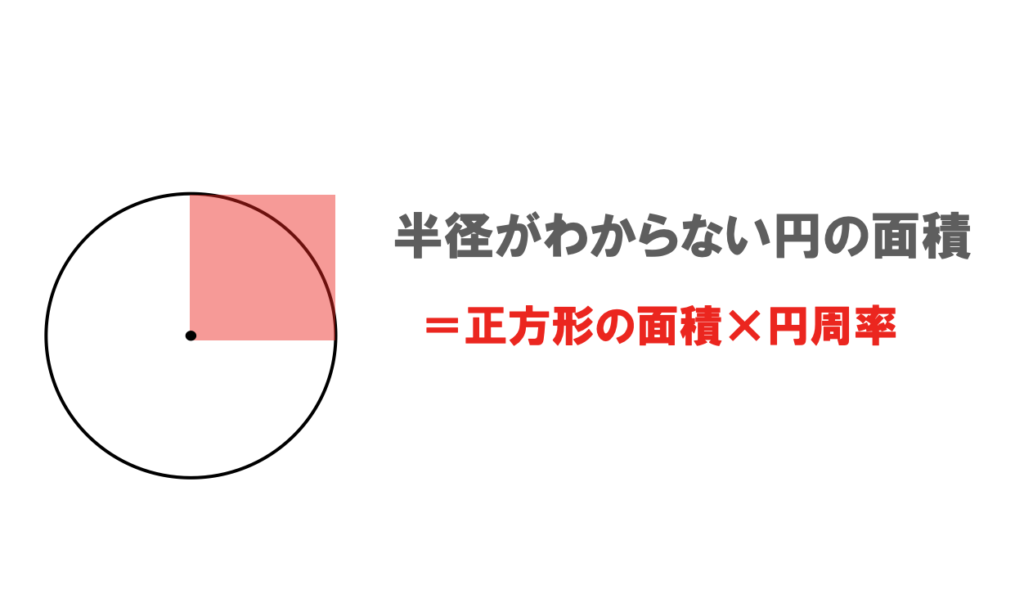
続いては「半径のわからない円やおうぎ形」の面積を求める場合です。
この場合、円の半径と正方形の１辺が等しくなるので、「半径×半径」＝「正方形の面積」になります。
それに「3.14」をかけると円の面積を求めることができるのです。
・差を求める場合は足す
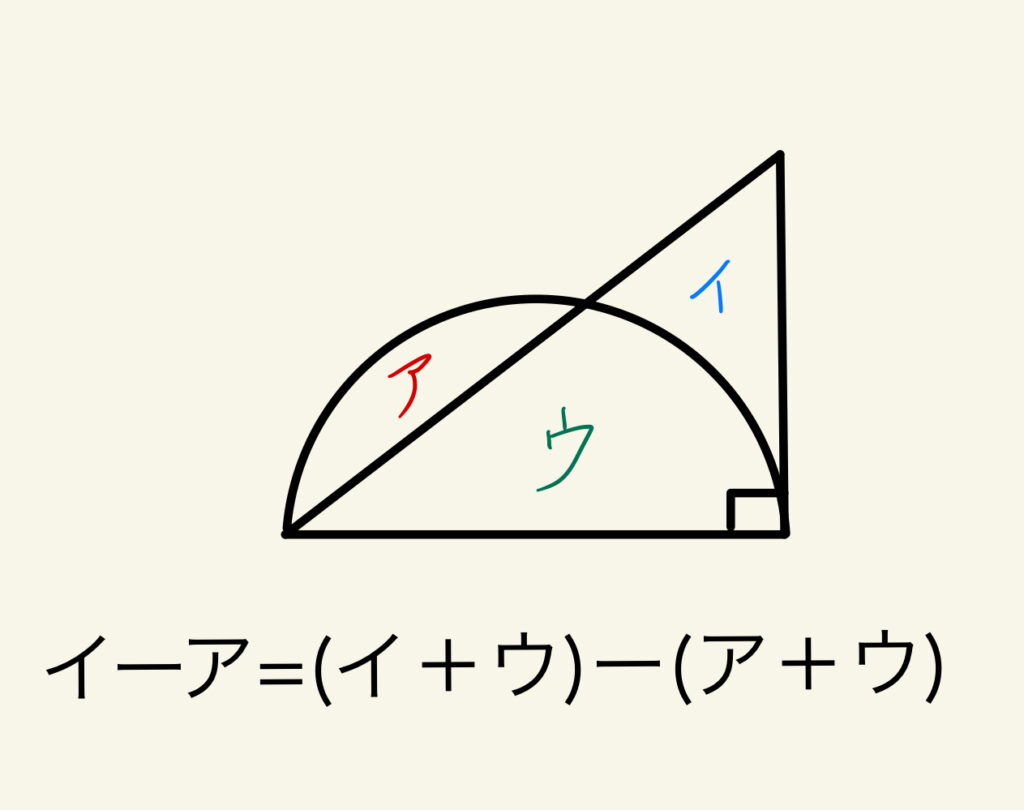
３つ目は面積の差を求める場合のコツです。
これは、先日の育成テストでも出題されていました。
「イ」の部分と「ア」の部分の差を求める場合、それぞれに「ウ」を足す方法です。
くっつけることで、面積の計算ができる基本図形ができるのです。
こうした図形を発見して解けたときは、とても気持ちいいよ！
まとめ
ここまで、算数の「面積」に強くなる秘訣をご紹介してきました。
面積の問題は「図形を把握する能力」と「計算をする能力」が求められます。
まずは公式を覚え、複雑な計算をすばやく解くことが得点力アップにつながると思います。
我が家では下記の問題集を購入して自宅学習に役立てています。
基本から応用まで幅広く問題が出題されているので、自宅学習にぴったりです。
解説も充実していて、入試によく出る問題が掲載されています。それに問題と答えが裏表になっているのもポイントが高いです。
最後になりますが、中学受験の成績を向上させるために「読書」は欠かせません。
我が家では「Kindle Unlimited」に加入していて、家族で読書を楽しんでいます。
月額980円で、200万冊以上のKindle電子書籍が読み放題になります。
スマホやタブレットがあればどこでも読むことができるし、中学受験向けの本も充実しています。
興味のある方は、30日間の無料体験がオススメです✨
- 30日間無料キャンペーン：30日間無料
最後まで読んでいただきありがとうございました。今後も役立つ情報を発信していきますので、よろしくお願いします。
にほんブログ村
